本文最后更新于 8 个月前,文中所描述的信息可能已发生改变。
一维插值
插值函数经过样本点,拟合函数一般基于最小二乘法尽量靠近所有样本点穿过。常见插值方法有拉格朗日插值法、分段插值法、样条插值法:
拉格朗日插值多项式:当节点数n较大时,拉格朗日插值多项式次数较高,可能收敛不一致,且计算复杂。 高次插值带来误差的震动现象称为龙格现象。
分段插值:虽然收敛,但光滑性较差。
样条插值:由于样条插值可以使用低阶多项式样条实现较小的插值误差,这样就避免了龙格现象。
线性插值与样条插值
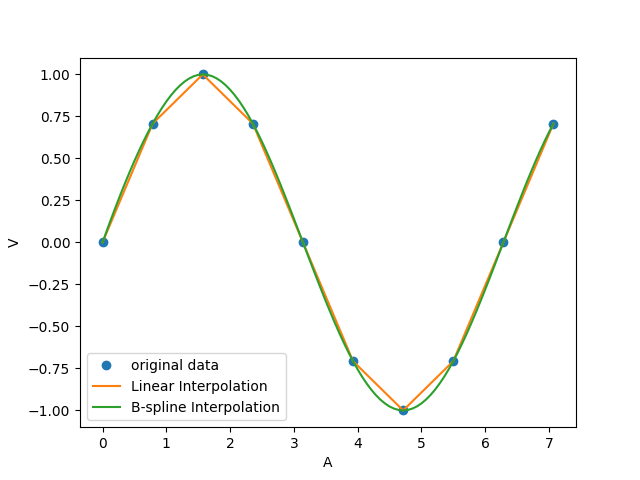
样例1:某电学元件的电压数据记录在0~2.25元A范围与电流关系满足正弦函数,分别用线性插值和样条插值方法给出经过数据点的数值逼近函数曲线。
代码:
python
import numpy as np
import pylab as pl
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi + np.pi / 4, 10)
y = np.sin(x)
x_new = np.linspace(0, 2 * np.pi + np.pi / 4, 100)
f_linear = interpolate.interp1d(x, y)
tck = interpolate.splrep(x, y)
y_bspline = interpolate.splev(x_new, tck)
# 可视化
plt.xlabel("A")
plt.ylabel("V")
plt.plot(x, y, "o", label="original data")
plt.plot(x_new, f_linear(x_new), label="Linear Interpolation")
plt.plot(x_new, y_bspline, label="B-spline Interpolation")
pl.legend()
pl.show()运行结果: