本文最后更新于 11 个月前，文中所描述的信息可能已发生改变。
一、实验内容
- 选择一组有意义的数据（不少于30个）或采用习题6中第4题数据；
- 计算该组数据的样本均值、顺序统计量、样本中位数、样本方差、样本标准差；
- 绘出频率直方图，经验分布函数图并进行简单分析说明.
二、准备工作
2.1 环境搭建
编程语言：R Language
集成开发环境（IDE）：Visual Studio Code
实验环境总览2.2 数据选取
根据题目要求，本实验选择习题6中第4题数据，数据内容如下：
| - | - | - | - | - | - | - | - | - | - |
|---|---|---|---|---|---|---|---|---|---|
| 15 | 20 | 15 | 20 | 25 | 25 | 30 | 15 | 30 | 25 |
| 15 | 30 | 25 | 35 | 30 | 35 | 20 | 35 | 30 | 25 |
| 20 | 30 | 20 | 25 | 35 | 30 | 25 | 20 | 30 | 25 |
| 35 | 25 | 15 | 25 | 35 | 25 | 25 | 30 | 35 | 25 |
| 35 | 20 | 30 | 30 | 15 | 30 | 40 | 30 | 40 | 15 |
| 25 | 40 | 20 | 25 | 20 | 15 | 20 | 25 | 25 | 40 |
| 25 | 25 | 40 | 35 | 25 | 30 | 20 | 35 | 20 | 15 |
| 35 | 25 | 25 | 30 | 25 | 30 | 25 | 30 | 43 | 25 |
| 43 | 22 | 20 | 23 | 20 | 25 | 15 | 25 | 20 | 25 |
| 30 | 43 | 35 | 45 | 30 | 45 | 30 | 45 | 45 | 35 |
三、实验主要步骤及结论
3.1 实验代码编写
实验中编写了如下图所示的代码
R
Score <- c(
15, 20, 15, 20, 25, 25, 30, 15, 30, 25,
15, 30, 25, 35, 30, 35, 20, 35, 30, 25,
20, 30, 20, 25, 35, 30, 25, 20, 30, 25,
35, 25, 15, 25, 35, 25, 25, 30, 35, 25,
35, 20, 30, 30, 15, 30, 40, 30, 40, 15,
25, 40, 20, 25, 20, 15, 20, 25, 25, 40,
25, 25, 40, 35, 25, 30, 20, 35, 20, 15,
35, 25, 25, 30, 25, 30, 25, 30, 43, 25,
43, 22, 20, 23, 20, 25, 15, 25, 20, 25,
30, 43, 35, 45, 30, 45, 30, 45, 45, 35
)
mean.Score <- mean(Score)
sort.Score <- sort(Score, decreasing = F)
median.Score <- median(Score)
var.Score <- var(Score)
sd.Score <- sd(Score)
hist(Score,
freq = F, main = "Frequency Histogram",
xlab = "Values", ylab = "Frequency", col = "#00ff00"
)
lines(density(Score), col = "#0088FF", lwd = 3)
x <- seq(from = 10, to = 100, by = 0.01)
lines(x, dnorm(x, mean(Score), sd(Score)), col = "red", lwd = 3)
print("") # 空函数，断点使用
plot(ecdf(Score),
verticals = T, do.p = F,
main = "Empirical Cumulative Distribution Function",
xlab = "Values", ylab = "Cumulative Probability",
col = "blue", lwd = 2
)
x <- seq(10, 100, 0.01)
lines(x, pnorm(x, mean(Score), sd(Score)), col = "red", lwd = 2)
print("") # 空函数，断点使用3.2 运行程序
使用R软件运行上述程序，得到运行结果列表如下：
| VARIABLES | VALUES |
|---|---|
mean.Score | 27.59 |
median.Score | 25 |
Score | num [1:100] 15 20 15 20 25 25 30 15 30 25 … |
sd.Score | 7.92272654832893 |
sort.Score | num [1:100] 15 15 15 15 15 15 15 15 15 15 … |
var.Score | 62.769595959596 |
x | num [1:9001] 10 10 10 10 10 … |
根据命令绘制成的图表如下所示：
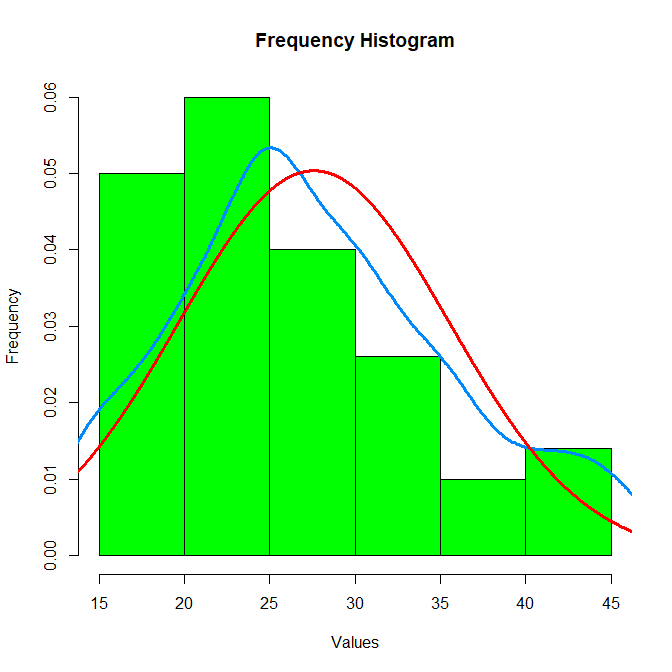Frequency Histogram
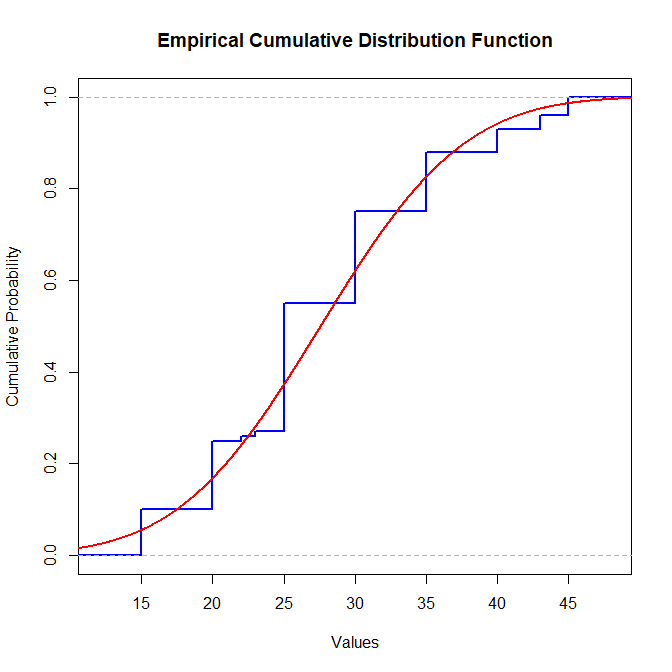Empirical Cumulative Distribution Function3.3 数据分析和实验结论
由上述数据值可以得到如下结论：
该组数据的样本平均值为：27.59；
样本中位数为：25；
样本方差为：62.77；
样本标准差为：7.927；
样本顺序统计量如下表所示：
- - - - - - - - - - 15 15 15 15 15 15 15 15 15 15 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 22 23 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 35 35 35 35 35 35 35 35 35 35 35 35 35 40 40 40 40 40 43 43 43 45 45 45 45
进一步对数据进行分析可得：
峰值的高度显示了数据点在这些峰值附近的集中度。数据点越密集的地方，峰值就越高。直方图中，
15-20、20-25和25-30的位置有很高的柱，说明数据点在这些位置有很多。数据值分布相对广泛，故数据的离散性相对较高。
经验分布函数图显示，数据值的累积随着数值的增长而增长，但不是完全符合正态分布的形状。这说明数据的分布有一些偏离正态分布的倾向。
